Comment, Errata and Omission That Did Not Make It To The Print
Page 47. Comment.
The proof is not a direct application of Theorem 4.5.15. It is a simple proof no doubt.
Once we can show that the limit of the middle function exists the proof is immediate. First note that if we have two functions m(x) and n(x) satisfying 0 £ m(x) £ n(x) for x ¹ a, and if 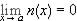 , then
, then 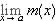 exists and
exists and 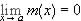 . This is immediate from the definition of limit.
. This is immediate from the definition of limit. 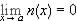 means that given any e > 0, we can find a d > 0 such that whenever 0 < | x - a| < d, we have that |n(x) - 0| = n(x) < e. Hence, whenever 0 < | x - a| < d, we have that |m(x) - 0| = m(x) £ n(x) < e. Therefore,
means that given any e > 0, we can find a d > 0 such that whenever 0 < | x - a| < d, we have that |n(x) - 0| = n(x) < e. Hence, whenever 0 < | x - a| < d, we have that |m(x) - 0| = m(x) £ n(x) < e. Therefore, 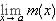 exists and
exists and 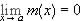 .
.
Now if for all x ¹ a, f (x) £ g(x) £ h(x), then 0 £ g(x) - f (x) £ h(x) - f (x). Since 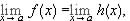
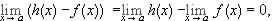 by the above argument, the limit
by the above argument, the limit 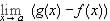 exists and so the limit
exists and so the limit 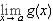 exists since
exists since 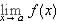 exists and g(x) = (g(x) - f (x)) + f (x). Therefore, by Theorem 4.5.15,
exists and g(x) = (g(x) - f (x)) + f (x). Therefore, by Theorem 4.5.15, 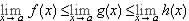 and so since
and so since 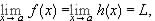
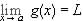 . Or
. Or 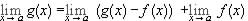 = 0 + L = L and we need not invoke Theorem 4.5.15.
= 0 + L = L and we need not invoke Theorem 4.5.15.
Page 55. In the Proof of Theorem 4.7.5. The following is omitted.
Now since f (b) = L, when g(x) = b, | f (g(x)) - L| = | f (b) - L| = 0 < e. Therefore, 0 < | x - a| < d implies that | f (g(x)) - L| < e. This completes the proof.
Page 143. Theorem 10.2.2.
Comment. A continuous and injective function on an interval is necessarily a continuous and monotonic function. So the hypothesis of Theorem 10.2.2 is the same as saying f is continuous and has an inverse function. See my web site for detail.
Page 215. Line 6. In the definition of the improper integral Definitions 13.3.3 (1), the lower limit of the integral on the right hand side should be "t" instead of "a". That is line 6 should be
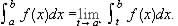
Page 218. Line 2: The minus sign in the equation should be a plus sign. I.e., line 2 should be
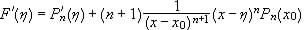 .
.
Line 4: There should be a minus sign in the right hand side of the equation. I.e., line 4 should be
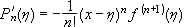 .
.
Page 220. Line -5. 13.5 The Proof of Theorem 13.2.1 should be preceded by the following sentence.
"It suffices to prove the result in the case of right limit. The proof for the left limit is similar. That being the case, the proof for the theorem then follows."
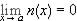 , then
, then 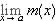 exists and
exists and 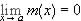 . This is immediate from the definition of limit.
. This is immediate from the definition of limit. 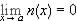 means that given any e > 0, we can find a d > 0 such that whenever 0 < | x - a| < d, we have that |n(x) - 0| = n(x) < e. Hence, whenever 0 < | x - a| < d, we have that |m(x) - 0| = m(x) £ n(x) < e. Therefore,
means that given any e > 0, we can find a d > 0 such that whenever 0 < | x - a| < d, we have that |n(x) - 0| = n(x) < e. Hence, whenever 0 < | x - a| < d, we have that |m(x) - 0| = m(x) £ n(x) < e. Therefore, 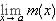 exists and
exists and 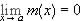 .
.
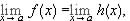
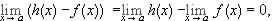 by the above argument, the limit
by the above argument, the limit 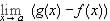 exists and so the limit
exists and so the limit 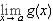 exists since
exists since 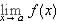 exists and g(x) = (g(x) - f (x)) + f (x). Therefore, by Theorem 4.5.15,
exists and g(x) = (g(x) - f (x)) + f (x). Therefore, by Theorem 4.5.15, 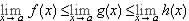 and so since
and so since 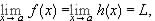
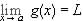 . Or
. Or 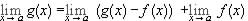 = 0 + L = L and we need not invoke Theorem 4.5.15.
= 0 + L = L and we need not invoke Theorem 4.5.15.
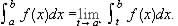
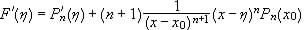 .
.
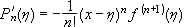 .
.